Computer Graphics Problem Solution: A Deep Dive into 2D Transformation

Computer Graphics Problem Solution: A Deep Dive into 2D Transformation

2D Transformation in Computer Graphics | 2D Translate Rotate object in Computer Graphics 🎮09

Hello and welcome, future graphics programmers! Professor Dr. Zeeshan Bhatti here from Zeeshan Academy. Today, we're rolling up our sleeves and tackling a problem that beautifully combines three fundamental pillars of 2D transformation: Shearing, Translation, and Rotation.

If you've ever wondered how objects move, twist, and reshape in digital space, you're in the right place. This isn't just about memorizing formulas; it's about understanding the journey a simple object takes through the magical world of linear algebra. So, grab a coffee, and let's get started!

Setting the Stage: What is a 2D Geometrical Transformation?

x' = 2 + (8 * 2) = 2 + 16 = 18
y' = 2 + (12 * 2) = 2 + 24 = 26

Therefore, V3' = (18, 26)

Important Note: Vertex V2 was not assigned a specific shear. Consequently, in this problem, we assume it remains unchanged for now. So, V2 remains (6, 2).

Our object, which was a small triangle, has now been dramatically stretched and skewed into a much larger, distorted triangle defined by V1' (36, 32), V2 (6, 2), and V3' (18, 26).

Graph of 2D Shear:
Imagine a small triangle near the origin getting pulled sharply to the right and upwards, resulting in a long, thin triangle. The point V1' is now far away in the top-right quadrant.

---

Transformation 2: The Simple Slide of 2D Translation

Next, we take our newly sheared object and move it. Translation is the simplest transformation; it's just a straight-up slide. Every point gets the same shift in the x and y directions.

The formula is: (x', y') = (x + tx, y + ty), where (tx, ty) is our translation vector, which is (5, -5).

We apply this to all three of our current vertices.

For V1' = (36, 32):

text

x' = 36 + 5 = 41
y' = 32 + (-5) = 27

Therefore, V1T = (41, 27)

For V2 = (6, 2):

text

x' = 6 + 5 = 11
y' = 2 + (-5) = -3

Therefore, V2T = (11, -3)

For V3' = (18, 26):

text

x' = 18 + 5 = 23
y' = 26 + (-5) = 21

Therefore, V3T = (23, 21)

Graph of 2D Translation:
The entire sheared triangle now shifts 5 units to the right and 5 units downwards. Notice how V2T has moved into negative Y-coordinate territory.

---

Transformation 3: The Elegant Turn of 2D Rotation

Finally, we add a spin to our object. Rotation is a bit more math-intensive, as it involves trigonometry. The formula to rotate a point (x, y) by an angle θ counter-clockwise about the origin is:

(x', y') = ( x*cos(θ) + y*sin(θ), -x*sin(θ) + y*cos(θ) )

Our angle θ is 35°. Let's pre-calculate the sine and cosine values to make our lives easier:

• cos(35°) ≈ 0.819

• sin(35°) ≈ 0.573

Now, let's rotate our three translated vertices.

For V1T = (41, 27):

text

x' = (41 * 0.819) + (27 * 0.573) = 33.579 + 15.471 = 49.05
y' = -(41 * 0.573) + (27 * 0.819) = -23.493 + 22.113 = -1.38

After rounding for simplicity: V1R ≈ (49, -1)

For V2T = (11, -3):

text

x' = (11 * 0.819) + (-3 * 0.573) = 9.009 + (-1.719) = 7.29
y' = -(11 * 0.573) + (-3 * 0.819) = -6.303 + (-2.457) = -8.76

After rounding for simplicity: V2R ≈ (7, -9)

For V3T = (23, 21):

text

x' = (23 * 0.819) + (21 * 0.573) = 18.837 + 12.033 = 30.87
y' = -(23 * 0.573) + (21 * 0.819) = -13.179 + 17.199 = 4.02

After rounding for simplicity: V3R ≈ (31, 4)

Graph of 2D Rotation:
The translated triangle now pivots 35 degrees around the origin (0,0). As a result, its final position is determined by V1R (49, -1), V2R (7, -9), and V3R (31, 4). You'll see the object has tilted and found its final resting place in the coordinate system.

---

Bringing It All Together: The Complete Workflow

Let's recap the incredible journey of our humble triangle:

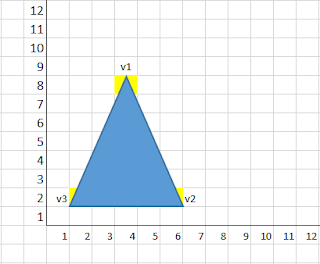
1. Original Object: V1(4,8), V2(6,2), V3(2,2)

2. After Shearing: V1'(36,32), V2(6,2), V3'(18,26)

3. After Translation: V1T(41,27), V2T(11,-3), V3T(23,21)

4. After Rotation: V1R(49,-1), V2R(7,-9), V3R(31,4)

To visualize this, you would plot the points at each stage and connect them to form the triangle. You would see a clear progression: a small triangle shears into a distorted shape, then slides to a new location, and finally rotates to its final orientation.

Why Does This Matter? The Bigger Picture in Computer Graphics

You might be thinking, "This is a lot of math for one triangle!" And you're right. However, these fundamental operations are the bedrock of everything you see in digital graphics.

• Video Games: When a character runs, their motion is a translation. When they turn, it's a rotation. When a spell distorts the environment, that's shearing and other complex transformations.

• Animation & CGI: Animators use these principles to create the illusion of movement and deformation for every character and object.

• UI/UX Design: When you open a menu that slides in, or an icon bounces, transformations are at work under the hood.

Furthermore, in real-world applications, we don't do these calculations one by one. Instead, we use transformation matrices to combine all these steps (shear, translate, rotate) into a single, efficient mathematical operation. This problem is the essential first step to understanding that more advanced topic.

Here is the Fianl Summary of What We have Learned and Some Problems for you to Solve.

2D Geometrical transformation is defined as, Let (A, B) be a straight line segment between the points A and B. Let T be a general 2D transformation. Then a T transforms can be applied on (A, B) into another straight line segment  to achieve (A’, B’), where:

   A’=TA and 

B’=TB

Problem: Consider an Object shown in figure below, what will be its new  Shape and Location after  Shearing of (4, 6) on vertex-1 and (8,12) on Vertex-3. The location is translated (5, -5) and Rotated (350). Draw the Graph also. 

 

2D Transformation in Computer Graphics | 2D Translate Rotate object in Computer Graphics 🎮09

Shear (x+ay, y+bx)

V1= (4,8), shear on V1 is (4,6)

  => (4+4x8,  8+6x4) 

  =  (36, 32)=V1`

V3= (2,2), shear on V3 is (8,12)

  => (2+8x2,  2+12x2)  

  = (18, 26)=V3`

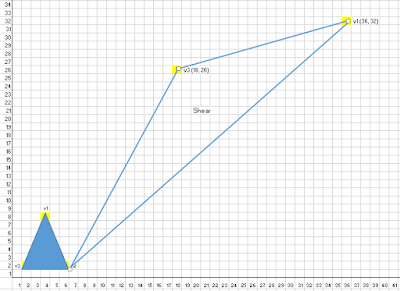Graph of 2D Shear

Translation of (5,-5) will be done on all three vertex. Here we will use New Vertex coordinates, V1`, V2, V3`.  

V1` = (36, 32) => (36+5, 32-5) 
      = (41, 27) = V1T

V2 = (6, 2) => (6+5, 2-5) 
      = (11, -3) = V2T

V3` = (18, 26) => (18+5, 26-5) 
      = (23, 21) = v3T

Graph of 2D Translation

Finally Rotation of 350 is performed again on three vertices, with their new location.

(x, y) => (x cos(q)+ysin(q), -x sin(q)+y cos(q) )

V1T = (41, 27) => (41 cos(35) +27sin(35) , -41sin(35) + 27cos(35) )

    => (( 41 x 0.819) + (27 x 0.573) , (-41 x 0.573) + (27 x 0.819) )

    =>  ( 33.579 + 15.471 , -23.493 + 22.113)

    V1R  => (49.05 , -1.38)  => 

     V1R = Roundoff( 49, -1)

V2T = (11, -3) => (11 cos(35) +-3sin(35) , -11sin(35) + -3cos(35) )

  => (( 11 x 0.819) + (-3 x 0.573) , (-11 x 0.573) + (-3 x 0.819) )

  =>  ( 9.009 + (-1.719) , -6.303 + (-2.457))

  V2R  => (7.29 , -8.76)  

 V2R = Roundoff( 7, -9)

V3T = (23, 21) => (23 cos(35) +21sin(35) , -23sin(35) + 21cos(35) )

  => (( 23 x 0.819) + (21 x 0.573) , (-23 x 0.573) + (21 x 0.819) )

  =>  ( 18.837 + 12.033 , -13.179 + 17.199)

  V3R  => (30.87 , 4.02)  

V3R = Roundoff( 31, 4)

  

Graph of 2D Rotation

Conclusion: You've Transformed Your Understanding!

Congratulations! You've successfully navigated a complex multi-step transformation problem. We started with a basic definition, moved through the practical calculations of shearing, translation, and rotation, and finally, we discussed the profound importance of these concepts.

The key takeaway is that every complex motion on your screen is a symphony of these simple 2D transformations. By mastering them, you're not just solving homework problems; you're learning the language of digital visuals.

If you want to see these graphs come to life and follow along with a visual demonstration, be sure to visit my YouTube channel, Zeeshan Academy. I have detailed video lectures that walk through these exact problems.

Keep practicing, and until next time, happy coding!

Instructor: Prof. Dr. Zeeshan Bhatti
YouTube Channel: Zeeshan Academy