Computer Graphics Hands-On Lab: Mastering Circle Drawing Algorithms in C++

Computer Graphics Hands-On Lab-2: Mastering Circle Drawing Algorithms in C++

By: Dr. Zeeshan Bhatti 

Focus Keyword: Circle Drawing Algorithms

Master the art of drawing perfect circles in computer graphics! This lab project by Dr. Zeeshan Bhatti guides you through Polynomial and Bresenham's Circle Algorithms in C++, with 7 practical tasks to build your skills.

Bresenham Circle Drawing Algorithm in Computer Graphics | Circle Drawing using Algorithm 🎮07 Part-1

Lab Objectives

Welcome to the graphics lab! This session is all about one of the most fundamental shapes in computer graphics: the circle. By the end of this lab, you will:

• Understand and implement the simple Polynomial method for circle drawing.

• Master the highly efficient Bresenham's Circle Drawing Algorithm.

• Learn how to utilize the symmetry of a circle to draw it efficiently.

• Gain practical experience in converting mathematical algorithms into C++ code with graphical output.

---

Lab Guidelines & Importance

This is a Lab project, to be done and submitted by each individual student during the Lab.

• Individual Work: Each student must complete the tasks individually.

• Submission: Print your Source Code and get it signed by the lecturer each week.

• Assessment: Lab projects carry marks that contribute to your final exam. The final Viva Voce will be based on these projects.

• Final Viva: You MUST bring all completed and signed Lab Project files to your final Viva Voce.

---

The Core Programming Tasks

We will use C++ with the Borland Graphics Interface (BGI) for simple graphical output. Ensure your IDE (like Turbo C++, Code::Blocks with WinBGIM) is set up correctly.

How to Solve Bresenham Line drawing in Computer Graphics | Bresenham Line Drawing method 🎮06 Part-2

---

Task 1: Draw a Circle using the Simple Polynomial Method

This method directly uses the circle equation: $x^2+y^2=R^2$. It's simple but inefficient because it uses floating-point calculations and a square root function.

Basic Algorithm:

text

For x = -R to R
    y = sqrt(R² - x²)
    PlotPixel(x, round(y))
    PlotPixel(x, -round(y))
End For

C++ Code Implementation:

cpp

#include <graphics.h>
#include <conio.h>
#include <iostream.h>
#include <math.h> // Required for sqrt() and round()

void main() {
    int gd = DETECT, gm;
    initgraph(&gd, &gm, "C:\\Turboc3\\BGI"); // Use your BGI path

    int x, y, radius;
    cout << "Enter the radius of the circle: ";
    cin >> radius;

    // Draw circle using polynomial method
    for (x = -radius; x <= radius; x++) {
        y = round(sqrt((radius * radius) - (x * x))); // Calculate y
        putpixel(x + 200, y + 200, WHITE);  // First octant (Shifted to center)
        putpixel(x + 200, -y + 200, WHITE); // Eighth octant
    }

    getch();
    closegraph();
}

Lab Questions:

1. Why is this method considered inefficient for computer graphics?

2. What is the purpose of adding 200 to the x and y coordinates in putpixel?

---

Task 2: Draw a Circle using Bresenham's Algorithm (All 8 Octants)

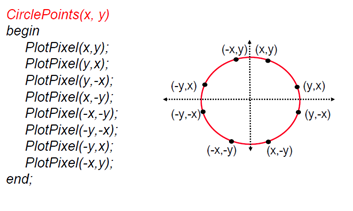
Bresenham's algorithm is a highly efficient, integer-only algorithm that uses circle symmetry. A circle is symmetric in all eight octants, so we calculate one octant and plot the other seven.

Circle Octants:

text

Octant 1: (x, y)      Octant 5: (-x, -y)
Octant 2: (y, x)      Octant 6: (-y, -x)
Octant 3: (-y, x)     Octant 7: (y, -x)
Octant 4: (-x, y)     Octant 8: (x, -y)

C++ Code Implementation:

cpp

#include <graphics.h>
#include <conio.h>
#include <iostream.h>

void main() {
    int gd = DETECT, gm;
    initgraph(&gd, &gm, "C:\\Turboc3\\BGI");

    int x_center, y_center, radius;
    cout << "Enter the center coordinates (x y): ";
    cin >> x_center >> y_center;
    cout << "Enter the radius of the circle: ";
    cin >> radius;

    int x = 0, y = radius;
    int d = 3 - (2 * radius); // Initial decision parameter

    // Loop to calculate points in the first octant
    while (x <= y) {
        // Plot points in all eight octants using symmetry
        putpixel(x_center + x, y_center + y, WHITE); // Octant 1
        putpixel(x_center + y, y_center + x, WHITE); // Octant 2
        putpixel(x_center - y, y_center + x, WHITE); // Octant 3
        putpixel(x_center - x, y_center + y, WHITE); // Octant 4
        putpixel(x_center - x, y_center - y, WHITE); // Octant 5
        putpixel(x_center - y, y_center - x, WHITE); // Octant 6
        putpixel(x_center + y, y_center - x, WHITE); // Octant 7
        putpixel(x_center + x, y_center - y, WHITE); // Octant 8

        if (d < 0) {
            d = d + (4 * x) + 6;
        } else {
            d = d + 4 * (x - y) + 10;
            y--;
        }
        x++;
    }

    getch();
    closegraph();
}

Lab Questions:

1. Explain the role of the decision parameter d in Bresenham's algorithm.

2. Why do we only calculate points until x <= y?

---

Bonus Challenge Tasks (C++ with BGI)

Ready to push your skills further? Here are 5 additional tasks to enhance your understanding.

---

Challenge 3: Animated Circle Drawing

Task: Modify Bresenham's algorithm to draw the circle slowly, showing how the points are plotted in sequence. Add a small delay after plotting each set of eight points.

Solution:

cpp

// Add after the include directives
#include <dos.h> // For delay()

// Inside the while loop, after the 8 putpixel statements, add:
delay(50); // 50 millisecond delay

---

Challenge 4: Concentric Circles

Task: Write a program that draws multiple concentric circles (circles with the same center but different radii).

Solution:

cpp

// After getting center coordinates
for (int r = 10; r <= 100; r += 10) {
    int x = 0, y = r;
    int d = 3 - (2 * r);
    
    while (x <= y) {
        // Use the same 8 putpixel calls as in Task 2
        // Change the color for visual effect: putpixel(..., r/10);
        x++;
        // ... rest of Bresenham's logic
    }
}

---

Challenge 5: Circle with User-Selected Algorithm

Task: Create a menu-driven program that asks the user which algorithm to use (Polynomial or Bresenham's) and then draws the circle accordingly.

Solution Outline:

cpp

void main() {
    // ... initgraph ...
    int choice;
    cout << "1. Polynomial Method\n2. Bresenham's Method\nEnter choice: ";
    cin >> choice;
    
    switch(choice) {
        case 1:
            // Call Polynomial method code
            break;
        case 2:
            // Call Bresenham's method code
            break;
        default:
            cout << "Invalid choice!";
    }
    getch();
    closegraph();
}

---

Challenge 6: Hollow Circle (Circle Outline Only)

Task: Modify Bresenham's algorithm to draw only the circle's outline without filling it. (Hint: You're already doing this! The challenge is to understand why this works).

Discussion: The basic Bresenham's algorithm naturally creates an outline because it only plots the boundary pixels. If you wanted to fill the circle, you would need to add code to draw horizontal lines between symmetric points.

---

Challenge 7: Colorful Circle Sectors

Task: Modify the circle drawing program to draw different octants in different colors.

Solution:

cpp

// In Bresenham's while loop, change putpixel colors:
putpixel(x_center + x, y_center + y, 1);  // Octant 1 - BLUE
putpixel(x_center + y, y_center + x, 2);  // Octant 2 - GREEN
putpixel(x_center - y, y_center + x, 3);  // Octant 3 - CYAN
putpixel(x_center - x, y_center + y, 4);  // Octant 4 - RED
putpixel(x_center - x, y_center - y, 5);  // Octant 5 - MAGENTA
putpixel(x_center - y, y_center - x, 6);  // Octant 6 - BROWN
putpixel(x_center + y, y_center - x, 7);  // Octant 7 - LIGHTGRAY
putpixel(x_center + x, y_center - y, 8);  // Octant 8 - DARKGRAY

---

MATLAB Implementation (For Reference)

Task 1 Solution in MATLAB:

matlab

% Simple Polynomial Circle Drawing in MATLAB
R = 50;
x = -R:1:R;
y = sqrt(R.^2 - x.^2);

plot(x, y, 'b.', x, -y, 'b.');
xlabel('x-axis'), ylabel('y-axis');
title('Circle Drawing using Polynomial Method');
grid on;
axis equal; % Important for proper circle proportions

---

Lab Submission Requirements

1. Source Code: Submit all .cpp files for Tasks 1, 2, and any bonus challenges you attempted.

2. Output Screenshots: Provide screenshots of the graphics window showing your circles for each task.

3. Answers: Include a separate document with answers to all "Lab Questions."

4. Signed Printouts: Bring printed copies of your code, signed by the lab instructor.

Remember: Consistent work in these labs forms the foundation for your final assessment. Don't fall behind!

Good luck, and happy circle drawing!

Instructor: Prof. Dr. Zeeshan Bhatti
YouTube Channel: Zeeshan Academy

Some Extra Tasks: 

Task 1: Draw the Circle using the simple Polynomial Method using CPP or JAVA

Basic Algorithm
For x= -R to R
      y = sqrt(R² - x²)
       PlotPixel(x, round(y) );
       PlotPixel(x, - round(y) );
end;

Solution in Matlab: 

x = 0;
R = 10;
R1 = -R;

x = R1 : 1 : R ;
y= sqrt(R.^2 - x.^2);

plot (x, y, '.' ,  x, -y , 'x' ), xlabel('x-axis'), ylabel('y-axis'), title('Draw Line Graph '), 
        grid off , axis([-10 10 -10 10]);


Task 2: Write the code for creating a Circle using Bresenhams Algorithm for all 8 octants.

NOTE: 

This is a Lab project, to be done and submitted by each individual student during the Lab, every week. Each student has to do the tasks given, print the Source Code, and get it signed by the lecturer during each lab. Each Lab project has Marks which will be given during the final exam, and the final Viva Vice will also be conducted from these lab projects. Therefore, Each student MUST complete these tasks individually and get it signed during the lab session and finally Must bring all the Lab Project files during the final Viva Vice for input of Marks.