Computer Graphics, Chapter 3: Solid Area (Polygon) Filling

Computer Graphics Demystified: Solid Area Polygon Filling and the Inside-Outside Test (Chapter-3)

- By: Prod. Dr. Zeeshan Bhatti

Bresenham Circle Drawing Algorithm in Computer Graphics | Circle Drawing using Algorithm 🎮07 Part-1

Hello and welcome back, future graphics experts! Professor Dr. Zeeshan Bhatti here from Zeeshan Academy. Today, we're tackling a fundamental question that sits at the heart of every digital image: How does a computer know which pixels to color inside a shape?

Whether you're looking at a simple button on a website or a complex character in a video game, the process of filling these shapes with color is governed by a set of clever algorithms known as Solid Area Polygon Filling. Let's dive in and decode this essential computer graphics concept.

Back to Basics: What Exactly is a Polygon?

Before we can fill anything, we need to understand what we're filling. In computer graphics, a polygon is defined as a chain of connected line segments. It's specified by a list of points called Vertices (or nodes), usually denoted as P₀, P₁, P₂, … Pₙ.

Think of it like connect-the-dots: the first vertex (P₀) is your starting point, and the last vertex (Pₙ) should connect back to P₀ to form a closed shape.

 

Figure-1: Polygons Shape Types

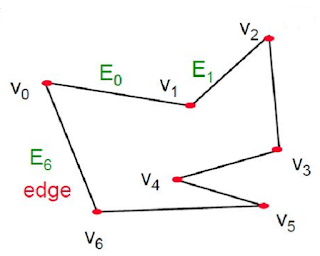
But there's more to it! A polygon is also often referred to as a MESH. This is because it's not just a single outline; it's a structure made up of multiple interconnected components:

• Vertex: A point where two or more edges meet. It's a location in 2D or 3D space (denoted as V1, P1, etc.).

• Edge: A straight line segment connecting two vertices (denoted as E1, E2, etc.). It's the boundary of the shape.

• Face (or Polygon): This is the closed area we're interested in! It's the interior surface enclosed by a loop of edges.

Understanding this mesh structure is crucial because when we talk about "filling a polygon," we are essentially talking about coloring all the pixels that lie within this face.

 

Figure-2: Polygon Mesh Showing Edges, Vertices, and Face.

The Core Question: How Do We Know What's Inside?

This leads us to the million-dollar question in rasterization: How do we know if a given pixel is inside or outside a polygon?

Imagine you have a complex, star-shaped polygon. For the computer to color it, it must test thousands of pixels on the screen, one by one, and make a simple decision: Is this pixel IN, or is it OUT?

The algorithms that perform this decision-making are called Inside-Outside Tests. These are the logical rules that define the interior of a polygon. Fortunately, there are two primary and elegant techniques for this.

Inside-Outside Test #1: The Odd-Even Rule (Even-Odd Rule)

This is the simpler of the two methods. Here's how you can visualize it:

1. Imagine drawing a line (called a scanline) from the pixel in question out to infinity in any direction (usually to the left or right for simplicity).

2. Now, count how many times this line crosses the polygon's boundary edges.

3. Apply the rule:

   • If the number of crossings is odd, the point is INSIDE.

   • If the number of crossings is even, the point is OUTSIDE.

Why does this work? Think of walking along your scanline. Every time you cross a boundary, you are essentially switching states: from outside to inside, or from inside to outside. An odd number of crosses means you ended up in the "inside" state.

Let's illustrate with an example: Consider a simple triangle. Take a point clearly in the center. If you shoot a ray to the left, it will cross exactly one edge (odd number), so it's inside. Now, take a point outside the triangle. A ray to the left might cross zero edges (even) or two edges (if it passes near a concave part), which is also even. In both outside cases, the rule holds.

This method is straightforward and computationally efficient, which is why it's widely used.

---

Inside-Outside Test #2: The Winding Number Method

The Winding Number method is a more powerful and nuanced approach. Instead of just counting crosses, it considers the direction in which the polygon edges are drawn.

Here's the concept:

1. Imagine you are standing at the point in question, and a string is tied to a tiny person walking along the polygon's boundary in the order its vertices are defined.

2. You keep track of how many times the person winds around you. Do they go counter-clockwise (usually considered positive) or clockwise (negative)?

3. The winding number is the total number of counter-clockwise revolutions around the point.

Now, apply the rule:

• If the winding number is non-zero (≠ 0), the point is INSIDE.

• If the winding number is zero (0), the point is OUTSIDE.

Why is this useful? The Winding Number method can better handle complex, self-intersecting polygons where the Odd-Even rule might produce ambiguous or undesirable results. It defines the interior based on which side of the edge the interior is, offering more control.

Analogy: Think of winding a key in a lock. If you wind it once (winding number = 1), you're engaged with the lock (inside). If you don't wind it at all, or your net winding is zero, you're not engaged (outside).

Odd-Even vs. Winding Number: A Quick Comparison

Feature	Odd-Even Rule	Winding Number Method
Logic	Counts edge crossings.	Counts net revolutions.
Complexity	Simpler and faster.	More computationally involved.
Best For	Simple, non-self-intersecting polygons.	Complex shapes and when specific fill styles are needed.
Result	Can be ambiguous for self-intersecting shapes.	Provides a more intuitive interior for complex shapes.

In most common applications, like filling the triangles that make up a 3D model, the Odd-Even rule is perfectly sufficient and is the go-to algorithm due to its speed.

From Test to Fill: The Scanline Fill Algorithm

Knowing how to test a single point is one thing, but testing every pixel on the screen would be incredibly slow. This is where efficient algorithms like the Scanline Fill Algorithm come in.

Instead of testing random points, this algorithm works systematically:

1. It works on a line-by-line (scanline) basis, moving from the bottom of the polygon to the top.

2. For each horizontal scanline, it calculates the intersections with all the polygon edges.

3. These intersection points are sorted from left to right.

4. Then, following the Odd-Even rule, it fills the pixels between pairs of intersections. For example, it fills between the first and second intersection, then between the third and fourth, and so on.

This method is highly efficient because it minimizes the number of calculations needed, leveraging coherence—the idea that pixels on a line are likely to have the same status as their neighbors.

Conclusion: The Invisible Engine of Digital Imagery

So, the next time you see a filled shape on your screen, remember the sophisticated logic working behind the scenes. From understanding the basic building blocks of a polygon mesh (vertices, edges, faces) to applying a logical Inside-Outside test (like the trusty Odd-Even Rule), the process of solid area filling is a beautiful blend of geometry and computer science.

These fundamentals are not just academic; they are the invisible engine that drives every raster-based image, from your desktop UI to the most advanced digital art.

To solidify your understanding, I highly recommend you download the full lecture slides which contain detailed diagrams and examples.

Download the Slides: Computer Graphics_Chapter 3 Solid Area Polygon Filling

In our next session, we'll start manipulating these polygons using 2D Geometrical Transformations—the magic of moving, rotating, and scaling objects. Stay tuned!

Keep creating, and I'll see you in the next lecture.

---

Instructor: Prof. Dr. Zeeshan Bhatti
YouTube Channel: Zeeshan Academy